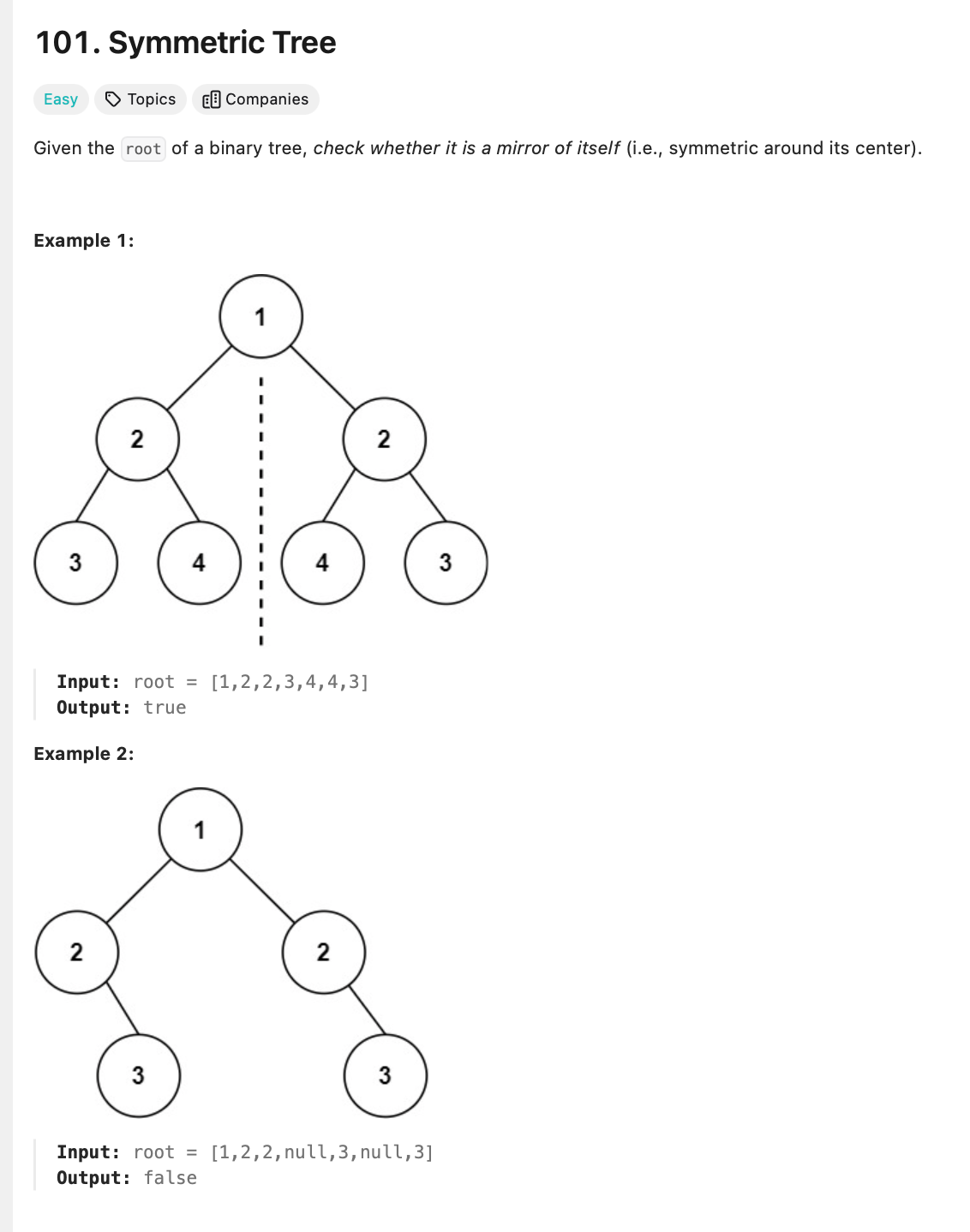
Symmetric Tree

The intuition behind the solution, followed by the implementation in algorithm form.

Intuition

My intuition started with the idea of folding along the axis - but, the properties that came to mind with trees are traversal, tree modification, and recursion.

Not folding the computer in half, hoping the leetcode problem will be solved.

It's not possible to actually fold a tree in half, unfortunately - so I need to use what exists in terms of properties (tree traversal, binary nature of trees, etc.), constraints (all levels have same values), knowledge (inorder gives values in order, hehe) to code a solution to something invisible.

Math

The 2 examples given have the same values in their levels. I'm assuming this is a feature. (1) I guess on an actual interview, you'd ask the interviewer.

I also see mirroring along the axis as an indication to look for asymmetry, because once we fold, the symmetry comes from asymmetry. (2)

The reverse is also true - if the 2 halves are symmetrical, then there's no mirroring. (3)

If I do an in order traversal of the left tree, I will get all the values in order of left child, root, right child, recursively applied. (4)

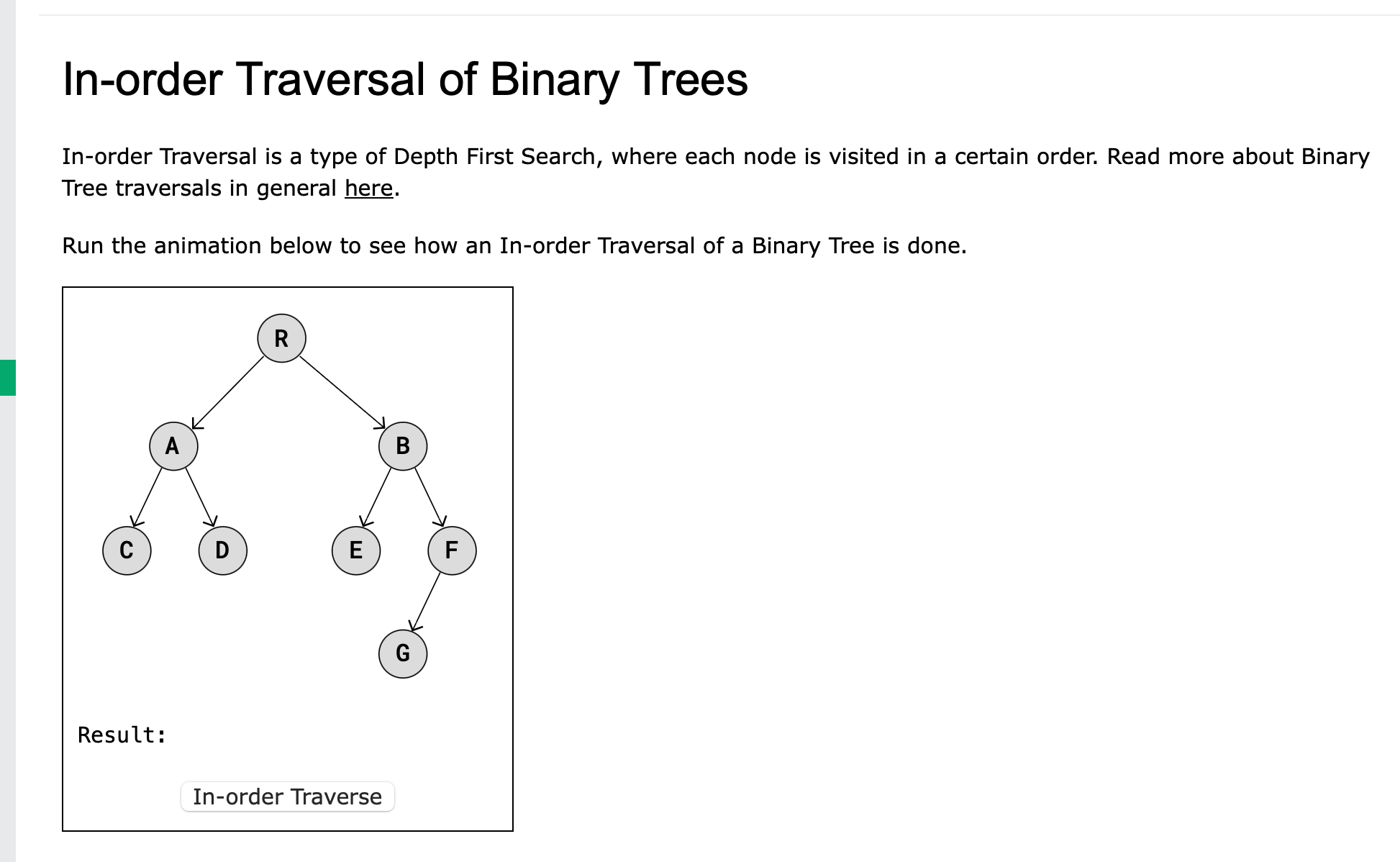
Combining these 4 assumptions, if the tree has mirrored subtrees, then an inorder traveral of the right subtree, should give me the opposite order of the left subtree.

If both are EXACTLY in reverse, then the tree is a mirror of itself - otherwise, it's not.

This algorithm is an algorithm, because it:

takes an input.

is finite.

Whether the arrays match (in reverse), is something we can quantify. It's a yes or no question.

Returning either true or false can terminate the algorithm.

is correct.

Getting an array inorder, is an existing technique.

If 2 things are opposite while being in order, then once, one is flipped, both will be the same.

The math makes sense!

is efficient.

Say, there are N nodes in a tree.

There will be (N-1)/2 nodes on the left, and the same amount on the right.

It's a binary tree, so I divided by 2.

I didn't count the root, on purpose - it's our base case, since a tree with a single node is always symmetrical.

Getting an array, inorder, will require (N-1)/2 of these:

1. Accessing a node, in a graph...To get to the bottom, you start at the top. 1 access per node.
2. Insert that value into an array which is 1 write.

The combined cost of getting a tree's contents, in order, is (N-1)/2 * 1 * 1

For 2 trees, it's 2 of these, one after the other:

(N-1)/2 * 1 * 1+(N-1)/2 * 1 * 1

As N goes to infinity, we have a cost of N.

Don't forget we need an array of minimum size, N/2, or just N in big o notation.

Unless there's a faster way to do this, this algorithm is maximally efficient.

If I were to work at a company, and investigate the above claim, knowing the solution would be more similar to computation analysis, and not coding.

Math likes exhaustive truths - when you say it's mostly true, the when matters. You can't call the on call team.

Math likes complete truths - when you say it's true, does that mean, the reverse is false?

Math likes truth.

Coding gets the job done, engineering builds things, but knowing the truth behind a statement, demonstrably so, makes the company look good in terms of Research & Development.

Such work may yield dividends down the road.

Unless the results of the proof directly impacts the product quality, it may not be worth the company's time, also.


Microsoft has a patent program.

Is there a faster way to do this?

Not for the intuition I had - because the idea of folding, requires me to get the values in order, which will always be the bottle neck.

I don't think there's a faster to verify symmetry, either - unless there's a way to be aware of the nodes, without actually visiting them.

So, if the problem has a constraint where I can stitch some parts of the tree, to another, traversal is not needed.

Then, we can lower the time cost by focusing on the idea of the trees being linked together, and we can rearrange them accordingly.

Linked structures - trees, linked lists, and graphs can be represented with pointers in memory, unlike arrays which rely on memory contuinity.

I assume you can implement any thing, any way you want, but the theoretical model of a linked list assumes it's easy to INSERT, especially at the end, but you go all the way to GET what's at the end.

The idea of an array, though, is that you can GET what you want at any time, but to insert, you have to UPDATE the whole thing MOST of the time.

I don't know if the idea of contiguous memory was developed because of these abstract models, the other way around, or both.

Did continuous hardware come first, for serial access, or did a theoretical model (an array, in this case) prompt engineers to arrange memory contiguously?

And, maybe you question whether there's a semantic relation between a GET in the API sense, and a GET in the 'oh, getting a value in an array, is o(1), if you know where to look'.

Whether a storage is distributed, or local, everything is binary, I guess.

Why is writing speed for RAM less than reading speed? And how do caches come into the picture?

Firstly, this is true, right? I feel that reads will always be faster than writes, also this guy here does some experiments to “prove” it. He doesn’t explain why, just mentions “caching issues”. (a…

Super Useruser2898278

In an engineering sense, someone can point out pre-storing the values in a tree - if that data is available immediately, then there's no need to traverse the tree.

This brings down the run time to o(1) - you just compare the 2 arrays.

If a program constantly needs to know if a tree is a mirror of itself, then overthinking speed and storage makes sense.

Leetcode's Solution

Leetcode's answer is behind a paywall, so I won't reproduce it here, except in summary.

The difference between their approach, and mine, is that theirs requires more sophisticated logic to compare both left and right trees.

In addition, their code compares sub trees as well - which is an important point, not mentioned in the question itself.

The question says, specifically:

Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

It's not in a riddle form, so there's no room for questioning, and no interviewer to confirm.

Riddle form

I have a tree.

If I fold it in the middle, will one cover the other, completely, like a scissors overlapping?

If I were to take a portion of the tree, will your answer apply to that portion, too?

How do you know so?

Do you have a train? Sorry

If the problem tests for subtree comparison, too, I think the question should be:

Given the root of a binary tree, check whether that tree, or any portion of that tree, is a mirror of itself (i.e., symmetric around its center).

Now, does my solution work for this unspecified constraint?

No, unfortunately.

This is because my algorithm statically compares one half of a tree, to another half of that tree.

The a and the the are always the uber tree, not any possible sub trees.

Also, even if I were to extend my solution to just generate inorder comparisons, for each subtree-pairing, such an action would add 2ⁿ time complexity.

This is because, the number of subtree-pairs, double every level - each node, can have 2 subtrees.

What do we do?

It's not that my algorithm has a complexity of 2ⁿ* n .

It has a complexity of n for a tree, assuming subtree comparison is not required.

It's funny, but also mathematically true - a good algorithm is defined by the problem, assuming we move down the logical chain, correctly.

Other than that, what can we do?

If this is a closed exam, and you already did the requirement gathering as best as you can....

Pray that you understand what is meant to be understood, and can code in a matter of milli seconds if you're wrong.