Pointers

I am using this site to study the problem patterns common in interviews.

Link to site, here:

LeetCode was HARD until I Learned these 15 Patterns

#21 - Patterns to master LeetCode

AlgoMaster NewsletterAshish Pratap Singh

Without further ado, this is pattern #2

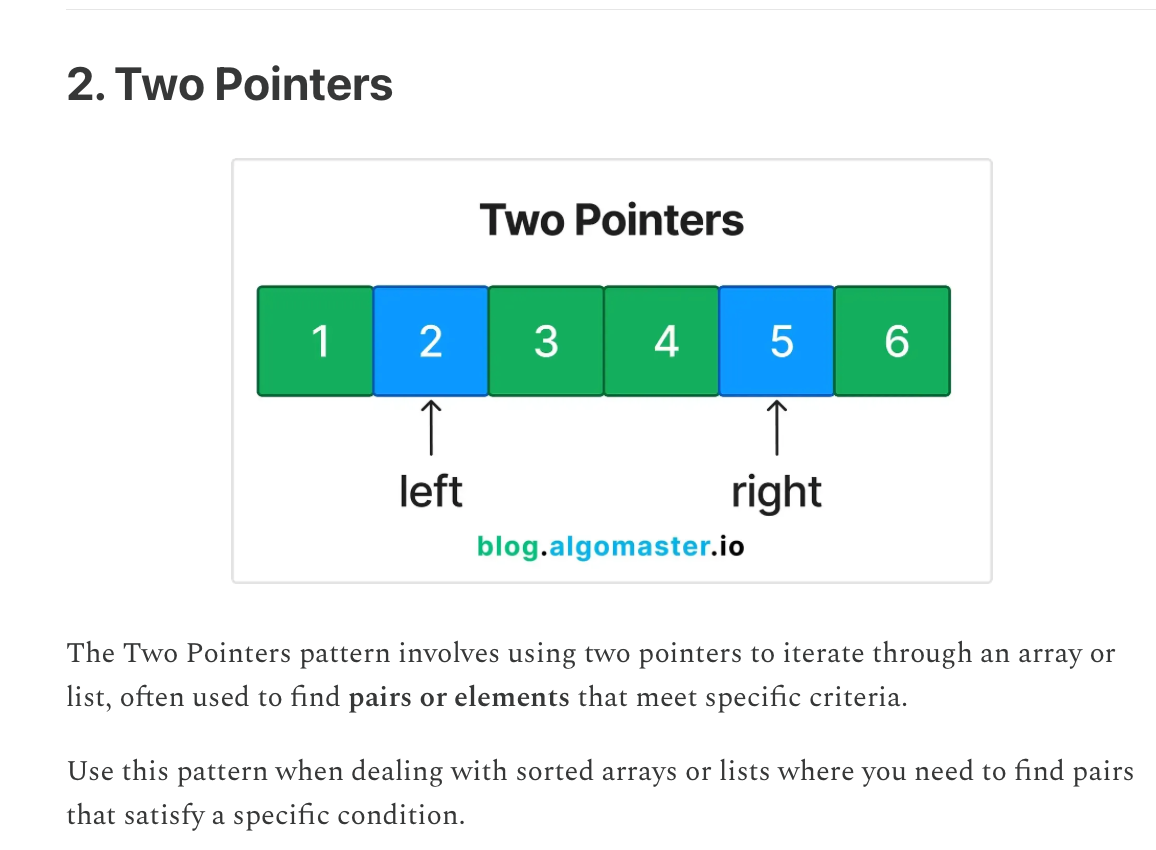
You've seen the concept of arrays before in my post on water buckets arrays - picture above is a array blue row of water buckets.

In that perspective, I focused on continuity - on how all the water buckets numbers are next to each other, and how this property lends itself to think about math.

Now, there is a type of algorithm called binary search.

It relies on the idea of dividing by half a lot, effectively reducing the problem more and more.

2 nice examples:

I asked my uncle as a young adult to guess which alphabet I was thinking of.

He said he at least needs a clue - he asked me if the alphabet he is thinking of is bigger or smaller than what I am thinking of.

He repeated this process, and won eventually, and quite unfortunately....

He used to work at Google - I guess he works at Alphabet now.

😆

There was this game I used to play as a child with my sisters where we were supposed to guess who was the culprit or something.

It was a board game with several people on the board.

The people could be opened or closed, depending on if they were a suspect or not.

You ask your opponent if the suspect has blue eyes, for example.

If she says no, you close all the people with blue eyes - else, you close everyone else.

I used to open by asking if the person was male or female - remove 50% at the get go.

My mother said she will always beat me in a game of mastermind (it's a game of logic and permutations).

Essentially the code has 4 colors, in 4 slots. The cracker needs that code.

The cracker (Amma) is allowed to ask questions to guess the nature of the code.

I can't lie, and there are rules that govern what is a good question - the idea being, eventually she should be able to guess the code, but not easily.

By eventually, I mean if you guess wrong, you lose a chance.

10 chances, total.

Instead of choosing red, blue, red, green, I chose something like, blue, blue, blue, blue.

I thought I was going to win!

It took Amma a lot of time, and 8 chances to figure out I chose all of the same color.

How is this all related to binary search?

The first 2 examples show a 'binary' way to eliminate branches. What my uncle did was pure binary search.

The second example isn't binary search, strictly - I can ask any yes / no question, but I thought it showed the point well.

The game of mastermind isn't related to binary search - I just wanted to boast. Once a parent assumes a 'normal case', children prey on the edge case.

Obviously my inability to go to Baskin Robbins now is different from my inability to go to Baskin Robbins 10 minutes ago....Techincally 10 minutes is more than 9 minutes.

Poor Amma.

But if binary is 2-based search, does a game of mastermind require 4-based search?

Quad search 🤯

Let's go back to pointers, and not get side tracked.

The way binary search works is we have 3 pointers - one at the beginning, one at the end, one at the middle.

Interviewer wants me to find X. I don't know what X is - but it's between 1 to 100.

I put a pointer at 1, another at 50, and the third at 100.

I ask if X is 50 - unlikely, but worth a shot. She says no. But X is smaller than 50.

Ok, then I make the middle, 25, and ending 50.

Is X 25?

No? It's bigger?

Ok, so the number is between 25 and 50.

I only consider this section - which is 75% less than 100 numbers.

So on and so forth, but as interesting as this story is, the story is not about what X is, or isn't.

It's about how pointers are used in binary search.

From a hardware perspective, pointers are needed to mark a memory location.

Arrays give immediate access - that is, in the water bucket analogy, I can immediately "see" which bucket has how much water.

You can't do this for a stack of plates in a wedding - you want the cleanest plate? You need to see all of them. Every plate has something on top. Some have tissues.

So I understand the benefit of pointers in these solutions - by changing what I refer to, I can do cool things that vary based on the current complication.

But what I find weird is this - binary search is basically a 2 pointer approach where you find the 'target' number by refining your search area, through iteration.

Note: I know my example uses 3 pointers, but the third pointer is an average of the other 2 - something I can ask the computer to do. (first + last / 2 => middle).

This doesn't affect the algorithm itself - it just shows I don't want go back and edit everything again 😭

2 different things are the same, in some ways.

Maybe I am confusing '2 pointer pattern' with 'Binary search algorithm', and deep in the dungeons of Saruman there is a difference between the 2.

But for now, it's just interesting 😄

My understanding of von-neumann architecture is that there is data, and data about data in a computer.

So an array of water levels (data), and an indication that this array lives somewhere in the 1s and 0s.

Or the example my mother said:

People live in houses, and houses have addresses - so a row of houses is an array of people, with their address being 'where to find them'.

I always hated that example from the bottom of my heart.

Here is a better one - water is in buckets, and buckets are in a row.

Anyway, algorithms are a way to manipulate these 2 data sets, maybe. 🤔

The correct algorithm, in the correct context, with smart assumptions can do a lot of work, fast.

Consider 2 algorithms I have in mind.

Problem: Boss has 100 servers. Which server of these has the size of 40 GB? All server sizes are given in ascending order.

I technically can randomly check 1 out of all servers. I have a 1% chance of finding the right number every time....

...and a 200% chance of increasing his stress.

My chances improve if I ask him 'Is this the number?' every time, but not by much.

Even if I remove the wrong number every time, I will still have the remainder to deal with.

50 steps later, my chances become 2%, and my boss is not very happy.

But if my algorithm is binary search, I can give him the server number he wants out of a 100, in no more than 7 steps.

1. First, I check the middle of 100. 50th server - the water level size is here not 40 GB.
   1. It's 120 GB.
2. Ok. Then, to server #25.
   1. Here, too, 110 GB is bigger than 40.
3. No? Then to server #12.
   1. Nope.
   2. 108 GB is bigger than 40.
4. server 6...
5. server 3?
6. server 1....Please, for the love of God.
   1. Oh ok, never mind.
   2. WE FOUND 40 GB!!!
7. 40 GB is in the very first server. Return 1, and get a promotion.

Why not return server #1, always?

If 40 GB is not even in the array, I can have the program return an error.

Plus, this way, I don't need to know what's in the array, nor the particular size the boss-man wants.

As long as I follow the approach of finding the correct subset to focus on, the program can handle 100 sizes, in ascending order, and find which one has size X.....always.

In return for more technique, I have a more flexible program. Since computers store these well, I don't really need to rewrite this again.

At that point, I am not a c# developer - I am a movie star.

If I write an algorithm, you can guess any number.... between 1 and 100.



I don't care.

I don't need to know the number.



If I write a program once, the algorithm works a million times.

Rajnipower. power of log_{base 2}.